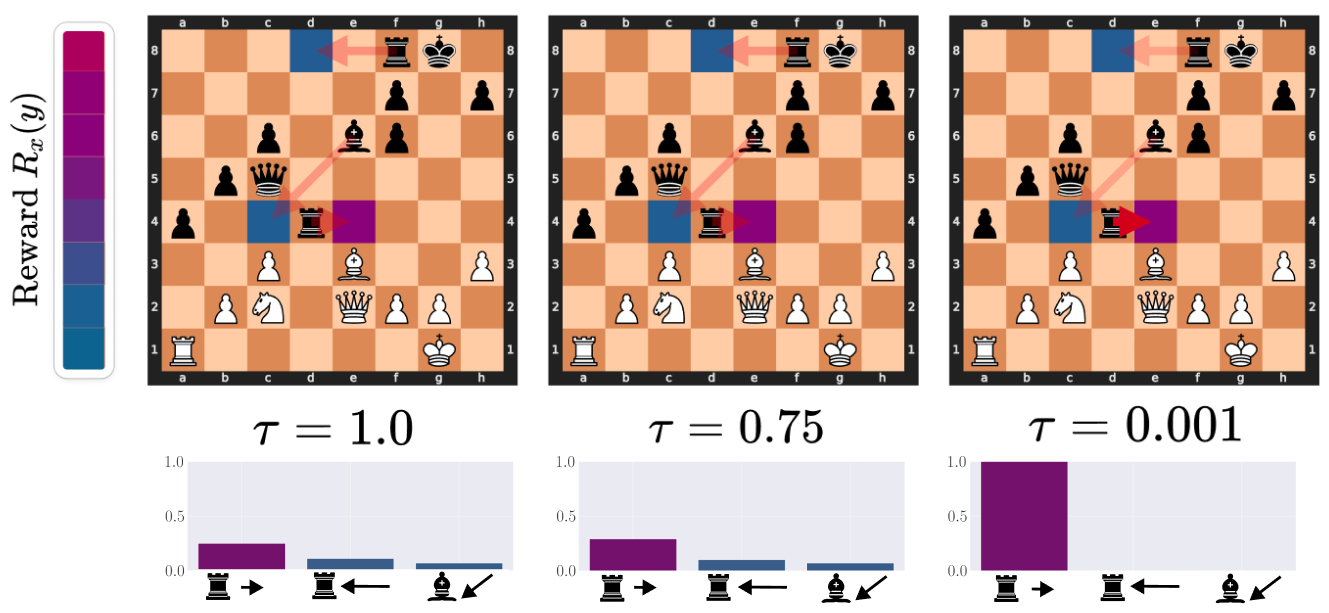
How Transcendence Works through Low-Temperature Sampling
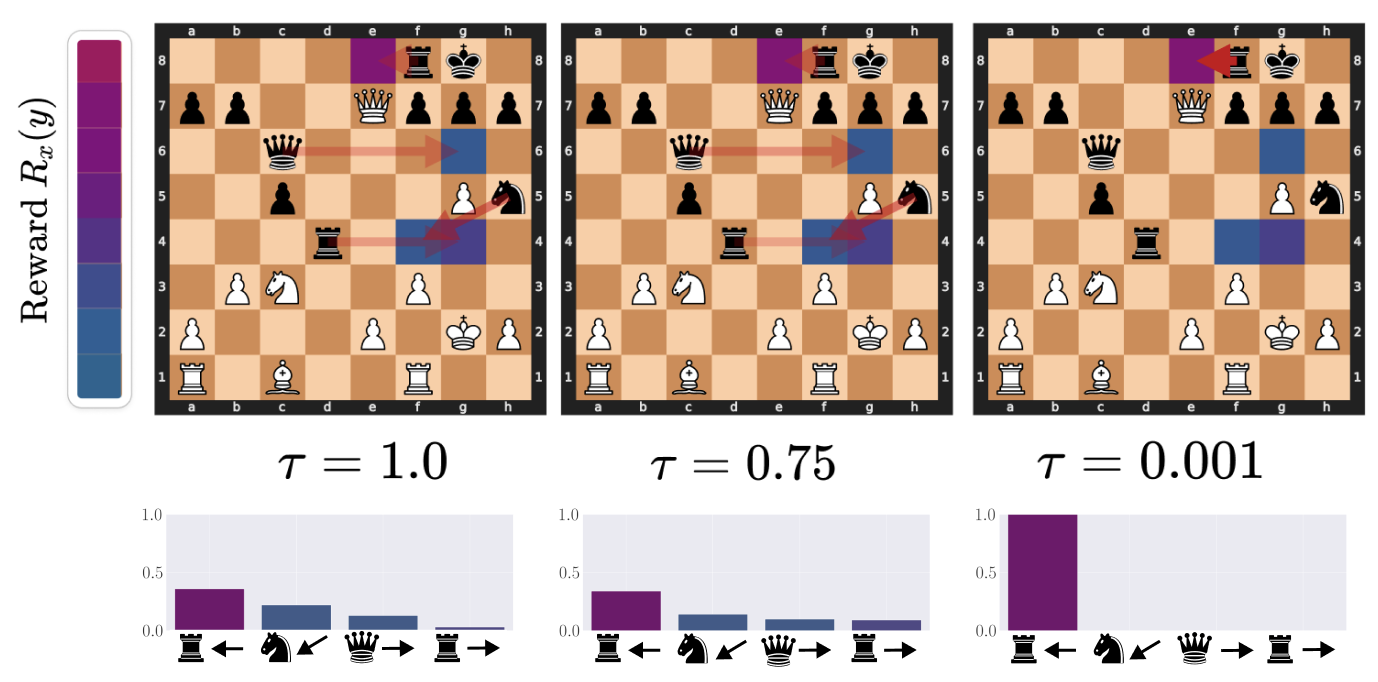
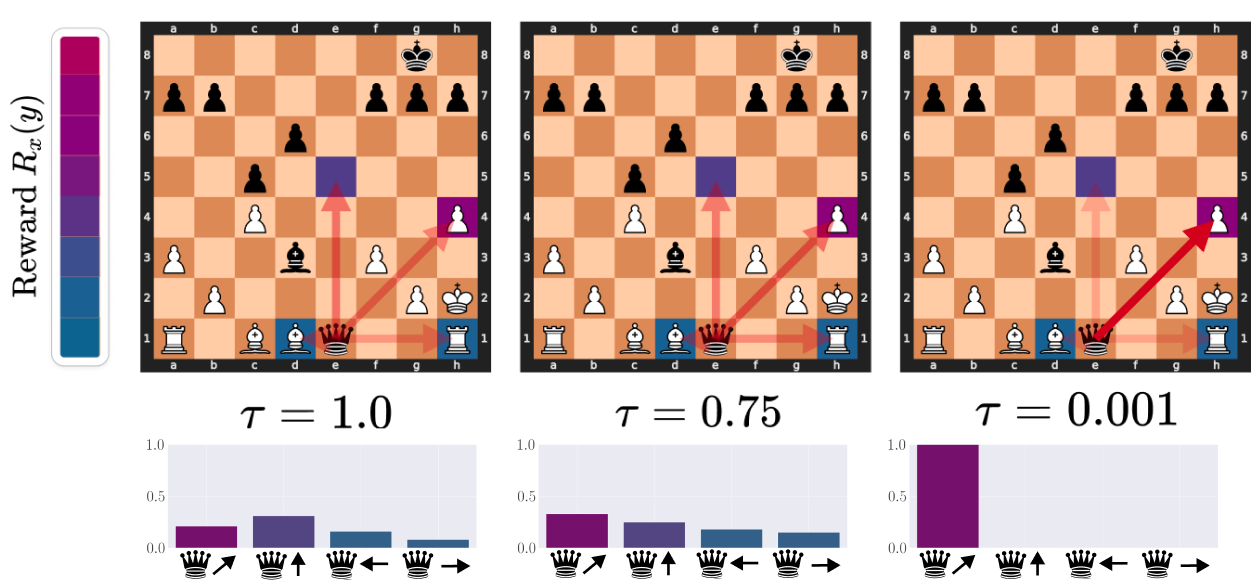
Visualizing the denoising effects of low temperature on the action distribution: an example of ChessFormer
shifting
probability mass towards the high reward move of trapping the queen with the rook as the temperature \( \tau \)
decreases.
Opacity of the red arrows represent the probability mass given to different moves. The color of the square
represent the
reward that would be given for taking the action that moves the given piece to that state. Purple here is high
reward,
while blue is low.
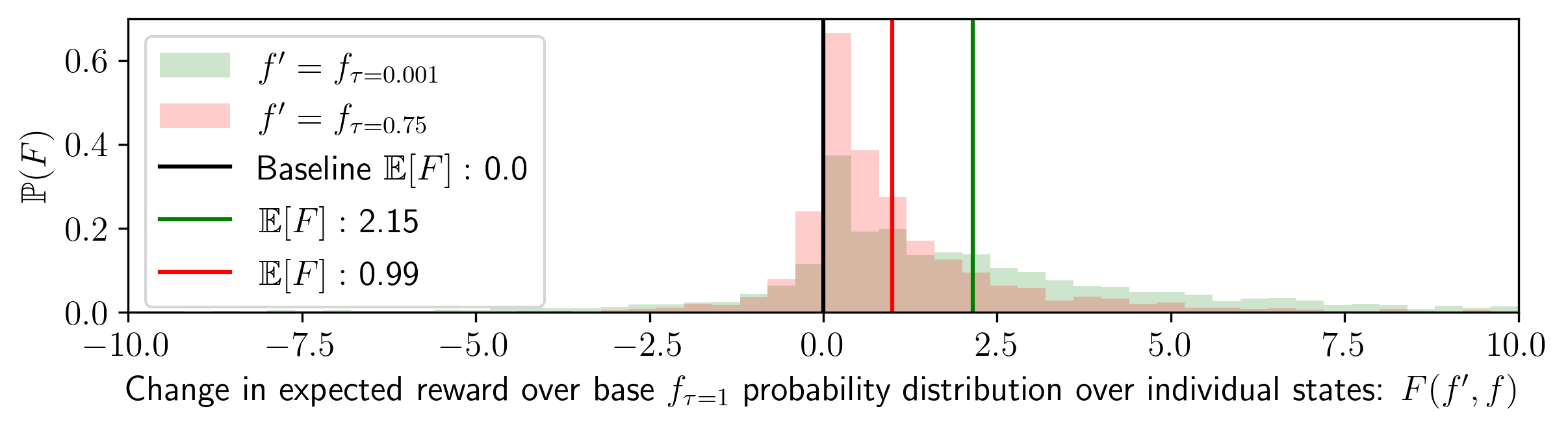
In the figure below, we plot the distribution of the change in expected reward across two different interventions:
setting
\( \tau
\rightarrow .75 \) and \( \tau \rightarrow 0.001 \) by
running the
Stockfish analysis engine across 100 games played at 0.001 temperature against Stockfish level 1, as well as
sampling 100 potential moves per move per game to gather an empirical probability distribution with n = 382100
total
samples per \( \tau \) (38.2 moves on average per game). We find that \( \tau \rightarrow 0.001 \) improves the
expected
reward (probability of winning) by an average of
2.17%, whilst \( \tau \rightarrow 0.75 \)
improves by
1.01%. Here, we define the "favor" of \( f' \) over \( f \) in \( x \) as the change in the reward function by
following some \( f' \) rather
than \( f \) for a given input \( x \): \( F(f', f ; x) = r_x(f') - r_x(f) \).
When Transcendence Happens
Formal Definition of Transcendence
In a setting of \( f_1, \dots, f_k \in \cf \) experts, \( \cx \) input
distribution, and \( p \in P(\cx) \), we define
transcendence to be:
\[
R_{p_{test}}(\hat{f}) > \max_{i \in [k]} R_{\ptest}(f_i).
\]
Here \( R_{\ptest}(f) \) is the expected reward of a predictor \( f \) on the test distribution \( \ptest \),
and \( r(x, y) \) is the reward function:
\[
R_{\ptest}(f) = \mathbb{E}_{x \sim \ptest}\left[r_x(f)\right], ~~~\mathrm{where}~~r_x(f) = \mathbb{E}_{y
\sim
f(\cdot |
x)} \left[r(x,y)\right].
\]
\[
R_{\ptest}(f) = \mathbb{E}_{x \sim \ptest}\left[r_x(f)\right],
\\
~~~\mathrm{where}~~r_x(f) = \mathbb{E}_{y
\sim
f(\cdot |
x)} \left[r(x,y)\right].
\]
In other words,
transcendence describes cases where the learned predictor performs better (achieves
better reward) than
the best expert generating the data.
Note that we are focusing on an idealized setting, where the learner has access to infinite amount of data
from the
distribution \( \dist \) , and can arbitrarily choose any function to fit the distribution (not limited to a
particular
choice of architecture or optimization constraints). As we will show, even in this idealized setting,
transcendence can
be impossible to achieve without further modifying the disribution.
Transcendence is possible with Low-Temperature Sampling
Now, we consider a temperature sampling scheme over the learned function \( \hat{f} \). Namely, for some
temperature \( \tau >
0 \), and some probability distribution \( q \in P(\cy) \), denote the softmax operator with temperature \(
\tau \) by
\( \softmax(q;\tau) \in P(\cy) \) such that
\[
\softmax(q; \tau)_y = \frac{\exp(q_y/\tau)}{\sum_{y' \in \cy}\exp(q_{y'}/\tau)}
\]
Additionally, we define \( \argmax(q) \in P(\cy) \) to be the uniform distribution over the maximal values of
\( q \),
namely
\[
\argmax{q} = \begin{cases}
1/|{Y_q}| & \mathrm{if}~y \in Y_q \\
0 & \mathrm{if}~y \notin Y_q
\end{cases}, ~~~\mathrm{where}~~~ Y_q = \{y \in \cy ~:~q_y = \max(q)\}
\]
\[
\argmax{q} = \begin{cases}
1/|{Y_q}| & \mathrm{if}~y \in Y_q \\
0 & \mathrm{if}~y \notin Y_q
\end{cases},\]
\[ ~~~\mathrm{where}~~~ Y_q = \{y \in \cy ~:~q_y = \max(q)\}
\]
Now, define \( \hat{f}_\tau \) to be the temperature sampling of \( \hat{f} \), i.e.
\[
\hat{f}_\tau(\cdot|x)
=
\softmax(\hat{f}
(\cdot|x);\tau)
\]
and \( \hat{f}_{\max} \) the arg-max ''sampling'' of \( \hat{f} \), i.e.
\[
\hat{f}_{\max}(\cdot|x) =
\argmax(\hat{f}(\cdot|x)).
\]
We prove in the paper that if the arg-max predictor \( \hat{f}_{\max} \) is better than
the best
expert,
then transcendence is possible with low-temperature sampling.
Assume that \( R_{\ptest}(\hat{f}_{\max}) > \max_{i \in [k]} R_{\ptest}(f_i) \), then there exists some
temperature \( \tau
\in (0,1) \) s.t. for all \( 0 \le \tau' \le \tau \) it holds that.
\[
R_{\ptest}(\hat{f}_{\tau'}) > \max_{i \in [k]} R_{\ptest}(f_i)
\]
Transcendence is possible with Diverse Datasets
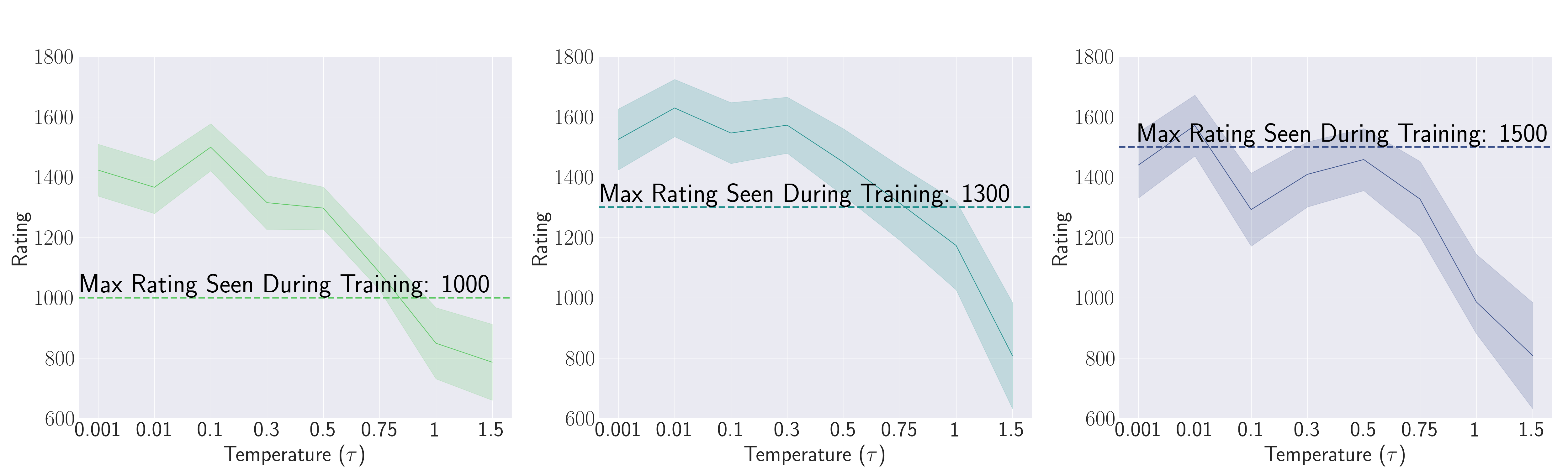
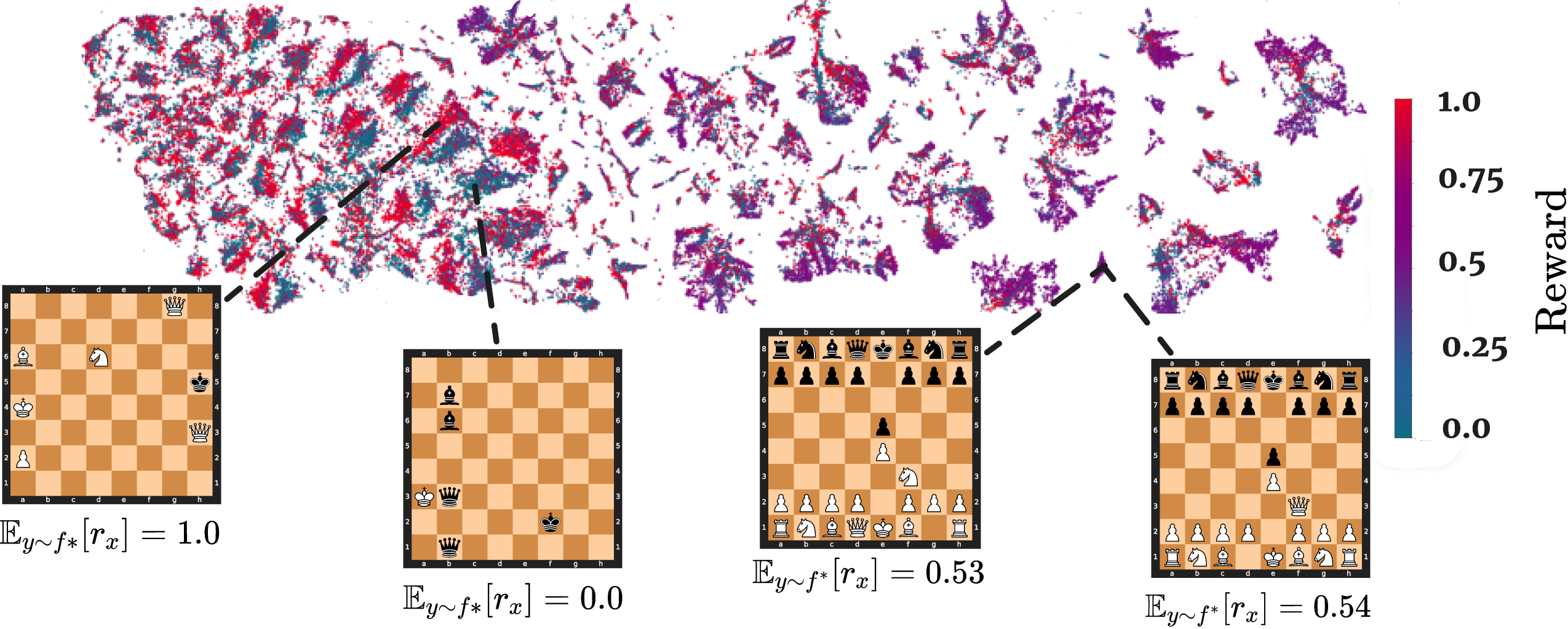
Our theory requires dataset diversity as a
necessary condition for enabling transcendence. As shown in the first figure, not all
models are able to transcend. Unlike ChessFormer 1000 or 1300, the Chessformer 1500 fails to transcend. We
hypothesize that this is due to the fact that in the band of ratings from 1000 to 1500, diversity does not
significantly increase. If this is true, a 1000 rated player can be thought of as a noisy 1500 rated
player, but a 1500 rated player cannot be thought of as a noisy 2000 rated player.
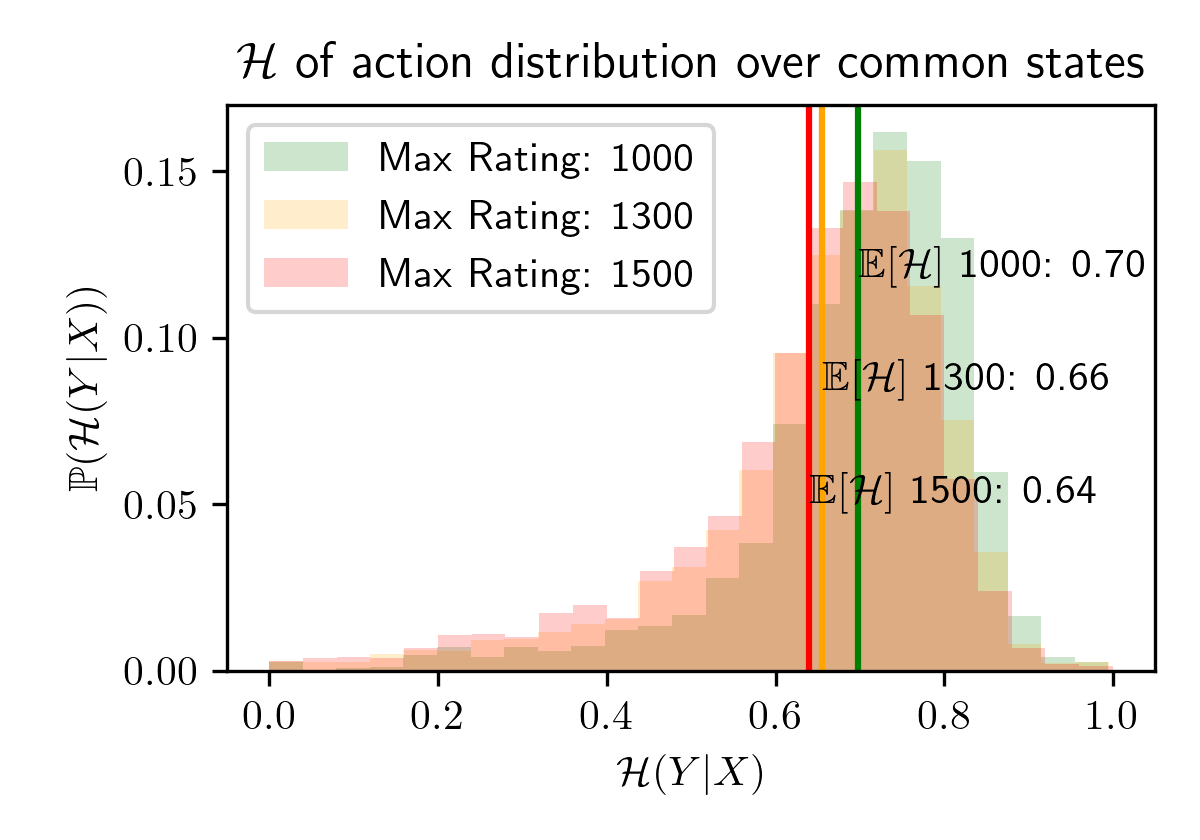
We explore this research question by quantifying dataset diversity through
the normalized entropy on the action distribution:
$$\mathcal{H}_f(Y | X)= {\mathbb{E}_{y \sim
f(y|x=X)}[-\log_2
f(y | x=X)]}/{\log_2 |\mathcal{Y}|}$$
\[
\mathcal{H}_f(Y | X)=\\
{\mathbb{E}_{y \sim
f(y|x=X)}[-\log_2
f(y | x=X)]}/{\log_2 |\mathcal{Y}|}
\]
To
gain intuition for this metric, imagine the action distribution of
moves taken for any given state. Entropy will be higher for more uniform action distributions, and lower for
more deterministic, peaked action distributions. The average entropy of these action distributions can
therefore serve as a measurement of the diversity of the dataset. We normalize this entropy to the range \([0,
1]\) by dividing by the binary log of the number of legal moves: \(\log_2 |\mathcal{Y}|\).
Importantly, we cannot calculate this normalized entropy for every state, as most states after move 16 in
the midgame and before the engame are unique within the dataset and we therefore observe just a single action
for thus states. Therefore our metric is limited in that it only considers opening moves, the beginning of the
midgame, and the endgame. We consider only common states with greater than 100 actions by sampling
1,000,000 games from each dataset. The average entropy confirm our hypothesis: The < 1500 cut off dataset
has on average less diversity than the < 1300 dataset, which has is again less than the < 1000 dataset.
This points towards answering our research question in the affirmative; Chessformer 1500 likely is not
transcendent due to a lack of diversity in its dataset. If the entropy stayed constant for each dataset,
this would imply a similar level of diversity for each. In such a case, we would expect that ChessFormer
1500 likely would also transcend. Instead, as predicted, Chessformer 1500 likely is not transcendent due
to a lack of diversity in its dataset.
Action distribution diversity, as measured by the average normalized entropy over different chess
rating dataset cutoffs with n = 2681, 3037, 3169 common states for ratings 1000, 1300, 1500, respectively.
These entropies are calculated directly from the empiricial frequencies of our dataset, and are model-agnostic.
t-SNE Embeddings of ChessFormer
Try zooming in by right clicking on the image, and click "Open Image in New Tab".
Inspired by
Deep Q-Networks (DQN) ,
we
generate a
t-SNE embedding of ChessFormer's
last
hidden
layer latent representations of game transcripts during training time. The colors represent the probability of
winning,
with +1 corresponding to a state where White has won and -1 to Black. We also visualize several board states
associated different clusters within the t-SNE embedding, and their associated expected reward when following
the
expert
Stockfish distribution.
Here, we generate a t-SNE embedding of
ChessFormer's last hidden layer latent representations of game transcripts during training time. The colors
represent the probability of winning, with +1 corresponding to a state where White has won and 0 to Black.
Probabiliy of winning is computed through the Stockfish analysis engine. We also visualize several board states
associated with different clusters in the t-SNE embedding, and their associated expected reward when following the
expert Stockfish distribution. Note that the model distinguishes between states where the outcome has already been
determined (the two left boards), versus opening states that are extremely similar (the two right boards).
We visualize the full TSNE again here, but this time coloring by game length rather than reward. We see that
games
with high reward tend to be longer, which makes logical sense as the result of the game will tend to be clearer
as
the game proogresses.
Additional Denoising Visualizations
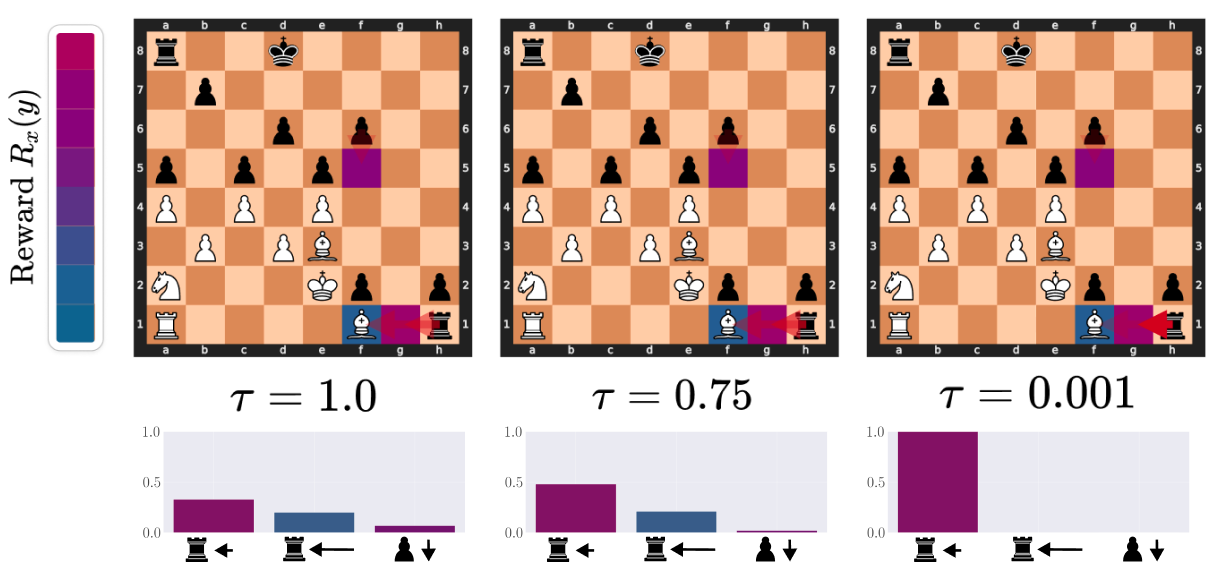
Here, we illustrate the importance of denoising. In the image below, denoising helps black find the only correct
move. White has pinned the black rook to
the Queen: any move where the rook does not move to e4 results in a heavy loss of material. As \(\tau\)
decreases,
the expected reward increases substantially and converges onto the correct move.
Another example where denoising helps avoid errors. Moving the queen to either d1 or h1 takes a bishop or rook,
respectively, but loses the queen in the following turn. While queen to e5 does not put the queen in immediate
danger,
it allows white to push the pawn on f3 to d3, where it threatens the queen and is protected by the bishop on c1.
The queen then must move out of danger, losing its opportunity to take the free pawn on h4 and giving white
valuable space towards the center of the board. As \(\tau\) decreases, the expected reward converges to the move
queen to d4, taking the pawn and checking the black king.
In this setup, a higher temperature shows two plausible moves for the black rook: g1 or f1. As the temperature
decreases, the expected reward converges to g1. If the black rook were to move to f1, the white rook would take
the black rook, blocking the black pawn on f2 from promoting and protecting the promotion square from the
h2 pawn. If the rook were to move to g1, on the other hand, it would open the promotion square from the h2 pawn
without being at any immediate risk. If white responded by moving its bishop to g2, protecting the promotion
squares
from both of the advanced black pawns, black could respond by taking the rook on a1, gaining significant material.
Intuition of Low Temperature Sampling Inducing Transcendence
To build intuition for the primary mechanism of transcendence that we explore in this work, we give the following
toy progression of distributions in order to clearly illustrate how low-temperature sampling can induce
transcendence through majority voting. Here, the middle purple action represents the correct, high-reward output,
whilst the left and right actions are low-reward, suboptimal outputs. We plot the probability of each output as a
label on
the x axis.
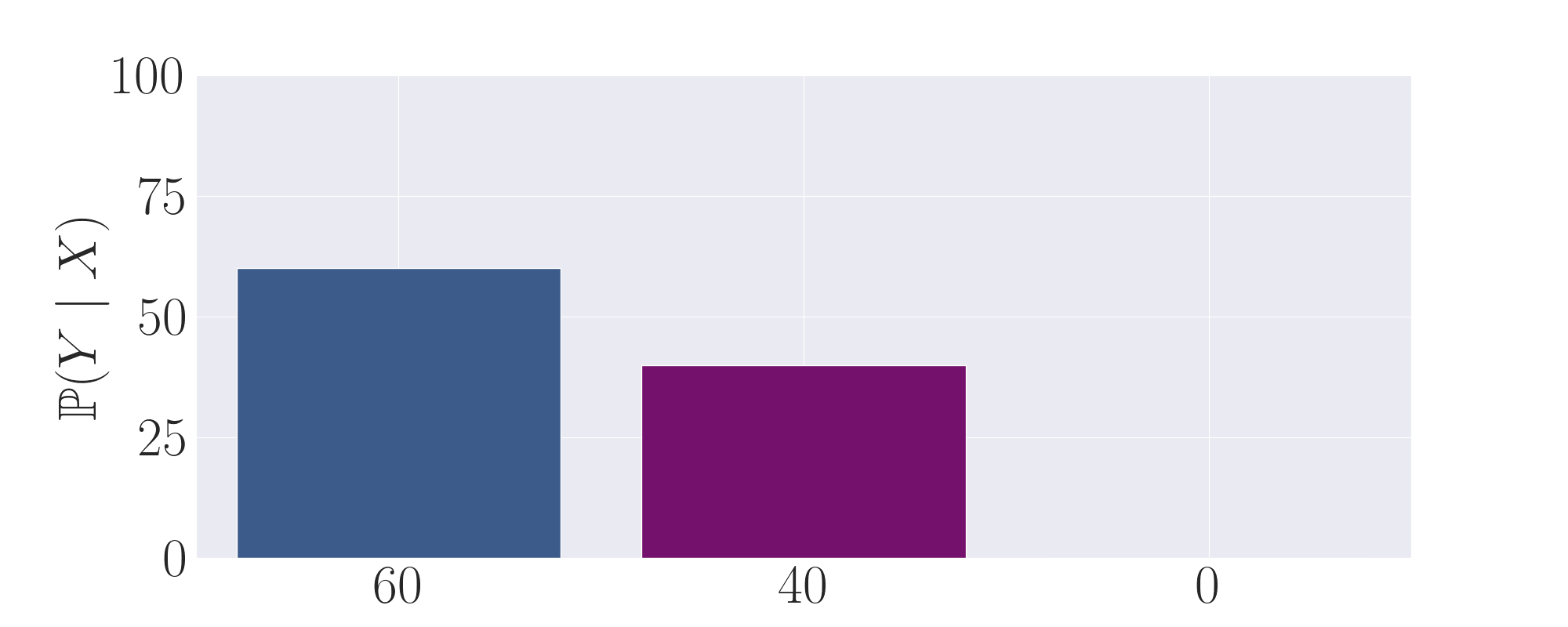
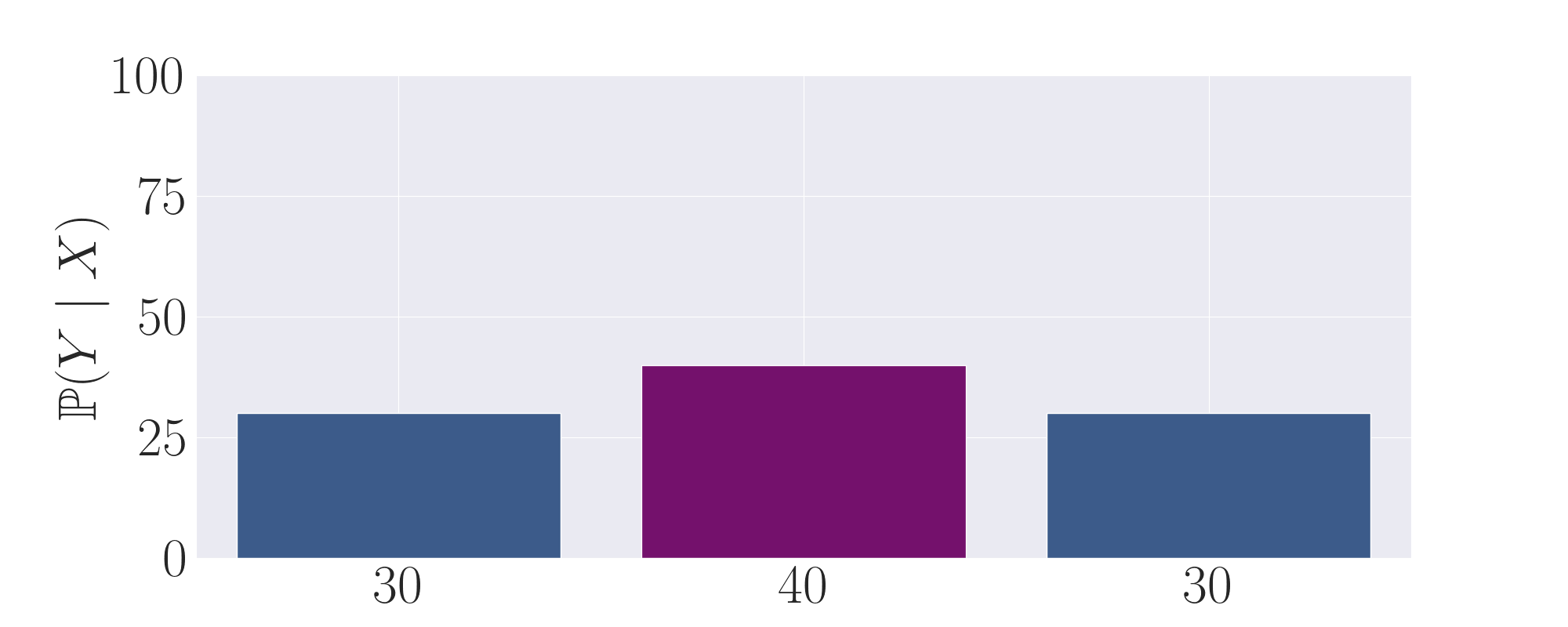
The first expert output distribution. Although it puts non-negligible mass on the purple, high-reward
action, it still samples a low-reward action the majority of the time.
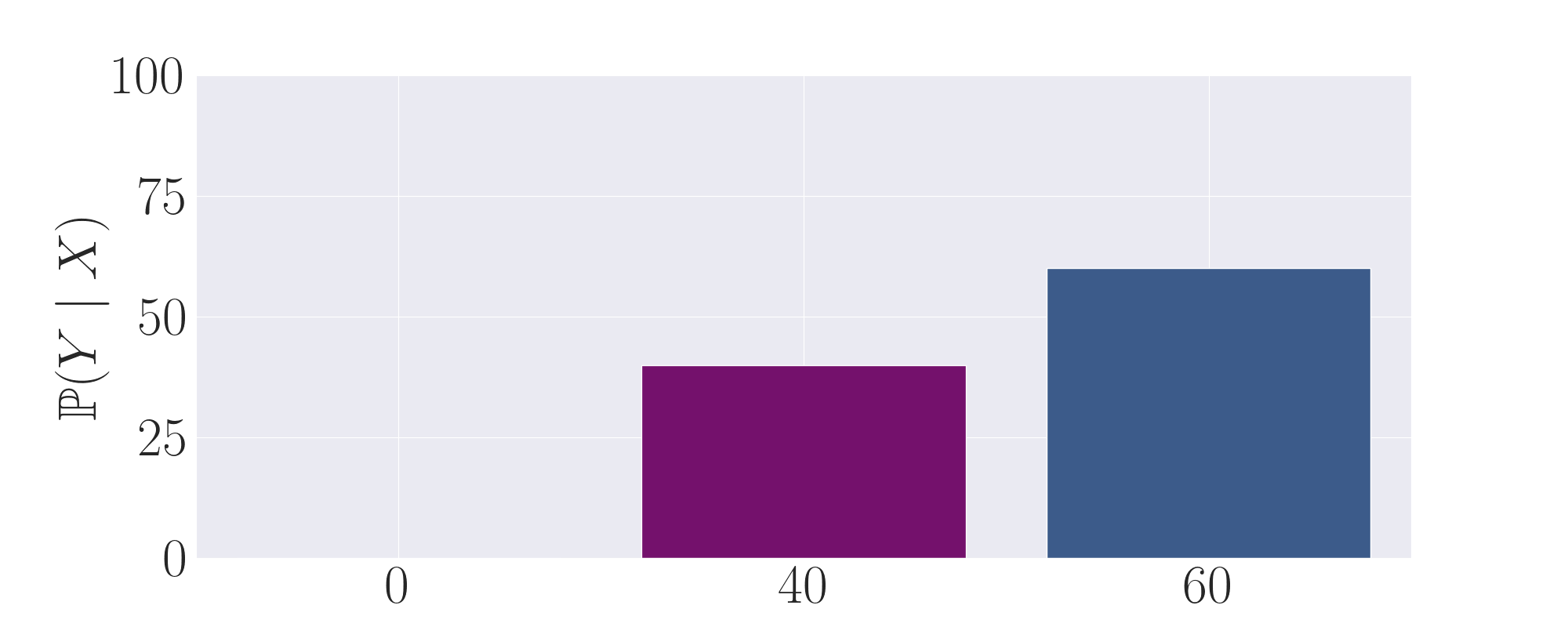
The second expert output distribution. Symmetric to the first expert, it also puts non-negligible mass
on the purple, high-reward action. However, it samples a low-reward action the majority of the time on the right.
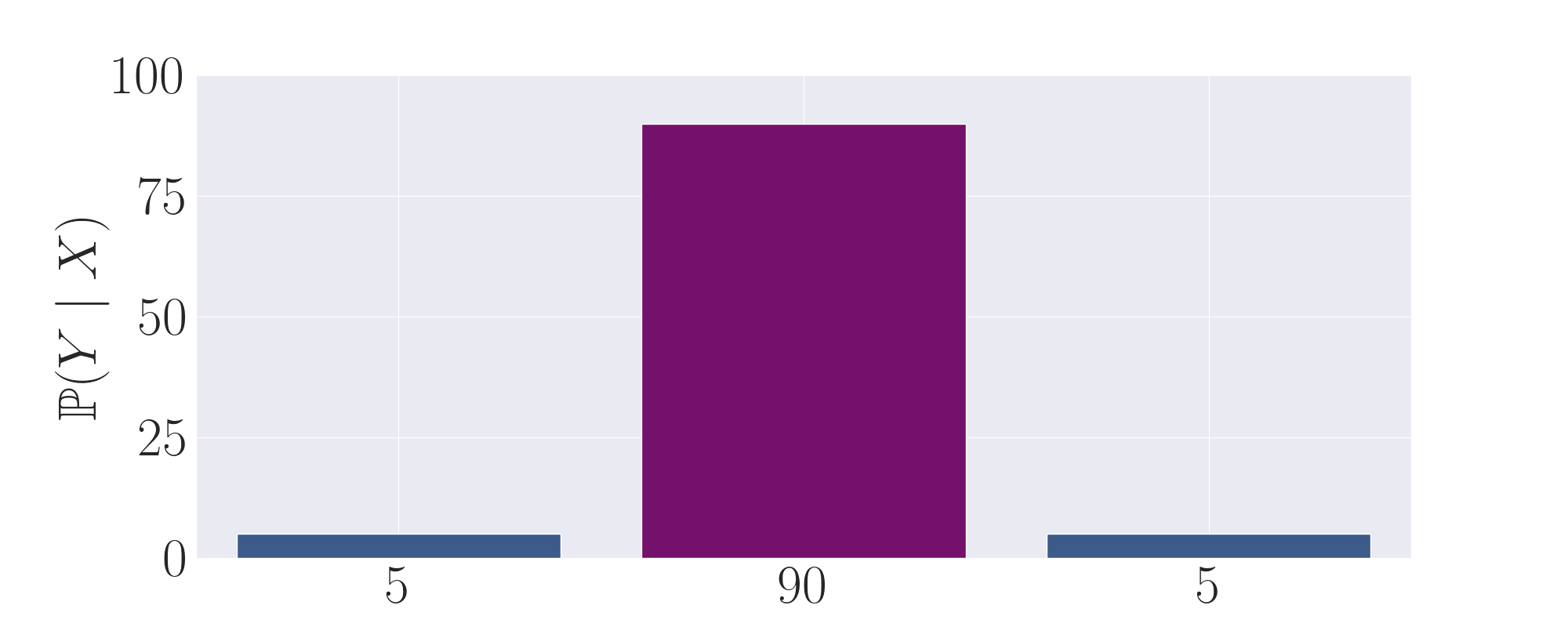
By taking the average of the first and second experts, we observe that this distribution now puts the majority of
mass onto the correct action.
Finally, by setting temperature \(\tau\) to be <1, more weight is shifted towards the high probability action,
leading to a gain in the expected reward.